Why 0.1 Is Not 0.1 In Python (Or Any Other Programming Language)

Humans have historically relied on their ten fingers — and sometimes toes — for rudimentary calculations, leading most cultures to adopt a decimal (base 10) numbering system, in which all numbers can be represented by the following formula:

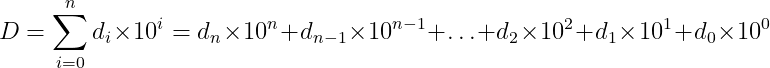
For example, 325 = 3×100 + 2×10 + 1×5. With the development of the first electronic computers, it was tempting to simply transfer this system to electronic circuits. In theory, this is possible by assigning ten integers to ten unique values of electrical current or voltage. However, practical issues such as temperature-sensitive resistances and electrical interference make this approach impractical. An alternative is to reduce complexity by using other numerical systems such as quintary (base-5) or ternary (base-3). However, the most robust and reliable system is binary (base-2), which simplifies states to just: "off" (0) and "on" (1), corresponding to the absence or presence of an electrical signal. In the binary system, numbers are represented by the following formula:

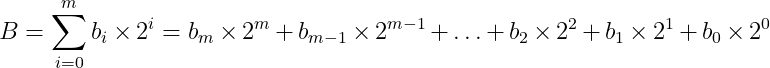
Data in digital computers is stored and organized in those binary digits, or bits. Typically, eight bits form a byte, which is the basic unit for storing a variety of data types, from simple numbers to complex multimedia. A major goal of computer science is to convert our diverse human data into this binary format for storage, computation, and retrieval. A byte, which is typically 8 bits long, can represent 2⁸ or 256 different values, allowing for a range from 0 to 255.

# Converting a decimal number to binary in Python
num = 13
binary_representation = bin(num)
print(f"The binary representation of {num} is {binary_representation[2:]}")

# Output: The binary representation of 42 is 101010

Representing our native decimal integers in binary is straightforward, as you can simply convert them. Fractional numbers are more challenging. For example, 0.125, which is also 1/8 (1/2³), translates cleanly into binary as 1/10¹¹. However, numbers like 0.1 (1/10) lack a finite binary representation and can only be approximated. This representation is called “floating point” or “float”. 

According to the IEEE 754 standard for floating-point arithmetic, these numbers are represented using a format that divides the binary representation into three parts: the sign (S), the exponent (E), and the fraction (F):

1. Sign bit (S): Determines whether the number is positive or negative. 0 for positive and 1 for negative.
2. Exponent (E): Used to calculate the power to which the base is raised.
3. Fraction (F) or Mantissa: Represents the precision bits of the number.

This format allows for the representation of a wide range of values, but can also introduce precision issues. Programming languages such as C++ allow users to specify the desired precision for approximating such numbers by choosing the appropriate type of floating-point number, which is typically available in sizes of 2, 4, 8, 16, or 32 bytes. Python defaults to 8-byte floats, which gives in an accuracy of about 16 decimal places. Representation of 0.1 according to the IEEE standard for floating-point arithmetic (IEEE 754):

Fractional number: 0.1

64-Bit (8-Byte) Binary Representation: 0011111110111001100110011001100110011001100110011001100110011010

Sign       (1 bit): 0
Exponent (11 bits): 01111111011
Fraction (52 bits): 1001100110011001100110011001100110011001100110011010

Reconverted Decimal (Exact): 0.100000000000000006

As we can see, the back-converted fractional number is not exactly 0.1. Granted, the difference is not large, but if we naively calculate with very small numbers without using appropriate Python packages, relevant inaccuracies can quickly creep in. But let's look at another example:

sum = 0
x = 0.1

for i in range(10):  
    sum += x  

if sum == 1:
    print(f"{sum} = 1.0 ")
else:
    print(f"{sum} is not 1.0 !?")

# Output: 0.9999999999999999 is not 1.0 !?

The result of this summation is now slightly less than 1, although we have seen that 0.1 is represented slightly larger than 0.1 according to IEEE 754 because Python had to round down in the intermediate steps.

The bottom line is that we should never lose sight of how the data types we use actually work under the hood. From fractions to letters, text, images, video, and sound, computer scientists have been finding elegant ways to represent the data of our analog world in the digital world for decades.